Multi-sample analyses
Last updated on 2024-11-12 | Edit this page
Overview
Questions
- How can we integrate data from multiple batches, samples, and studies?
- How can we identify differentially expressed genes between experimental conditions for each cell type?
- How can we identify changes in cell type abundance between experimental conditions?
Objectives
- Correct batch effects and diagnose potential problems such as over-correction.
- Perform differential expression comparisons between conditions based on pseudo-bulk samples.
- Perform differential abundance comparisons between conditions.
Setup and data exploration
As before, we will use the the wild-type data from the Tal1 chimera experiment:
- Sample 5: E8.5 injected cells (tomato positive), pool 3
- Sample 6: E8.5 host cells (tomato negative), pool 3
- Sample 7: E8.5 injected cells (tomato positive), pool 4
- Sample 8: E8.5 host cells (tomato negative), pool 4
- Sample 9: E8.5 injected cells (tomato positive), pool 5
- Sample 10: E8.5 host cells (tomato negative), pool 5
Note that this is a paired design in which for each biological replicate (pool 3, 4, and 5), we have both host and injected cells.
We start by loading the data and doing a quick exploratory analysis,
essentially applying the normalization and visualization techniques that
we have seen in the previous lectures to all samples. Note that this
time we’re selecting samples 5 to 10, not just 5 by itself. Also note
the type = "processed" argument: we are explicitly
selecting the version of the data that has already been QC
processed.
R
library(MouseGastrulationData)
library(batchelor)
library(edgeR)
library(scater)
library(ggplot2)
library(scran)
library(pheatmap)
library(scuttle)
sce <- WTChimeraData(samples = 5:10, type = "processed")
sce
OUTPUT
class: SingleCellExperiment
dim: 29453 20935
metadata(0):
assays(1): counts
rownames(29453): ENSMUSG00000051951 ENSMUSG00000089699 ...
ENSMUSG00000095742 tomato-td
rowData names(2): ENSEMBL SYMBOL
colnames(20935): cell_9769 cell_9770 ... cell_30702 cell_30703
colData names(11): cell barcode ... doub.density sizeFactor
reducedDimNames(2): pca.corrected.E7.5 pca.corrected.E8.5
mainExpName: NULL
altExpNames(0):R
colData(sce)
OUTPUT
DataFrame with 20935 rows and 11 columns
cell barcode sample stage tomato
<character> <character> <integer> <character> <logical>
cell_9769 cell_9769 AAACCTGAGACTGTAA 5 E8.5 TRUE
cell_9770 cell_9770 AAACCTGAGATGCCTT 5 E8.5 TRUE
cell_9771 cell_9771 AAACCTGAGCAGCCTC 5 E8.5 TRUE
cell_9772 cell_9772 AAACCTGCATACTCTT 5 E8.5 TRUE
cell_9773 cell_9773 AAACGGGTCAACACCA 5 E8.5 TRUE
... ... ... ... ... ...
cell_30699 cell_30699 TTTGTCACAGCTCGCA 10 E8.5 FALSE
cell_30700 cell_30700 TTTGTCAGTCTAGTCA 10 E8.5 FALSE
cell_30701 cell_30701 TTTGTCATCATCGGAT 10 E8.5 FALSE
cell_30702 cell_30702 TTTGTCATCATTATCC 10 E8.5 FALSE
cell_30703 cell_30703 TTTGTCATCCCATTTA 10 E8.5 FALSE
pool stage.mapped celltype.mapped closest.cell
<integer> <character> <character> <character>
cell_9769 3 E8.25 Mesenchyme cell_24159
cell_9770 3 E8.5 Endothelium cell_96660
cell_9771 3 E8.5 Allantois cell_134982
cell_9772 3 E8.5 Erythroid3 cell_133892
cell_9773 3 E8.25 Erythroid1 cell_76296
... ... ... ... ...
cell_30699 5 E8.5 Erythroid3 cell_38810
cell_30700 5 E8.5 Surface ectoderm cell_38588
cell_30701 5 E8.25 Forebrain/Midbrain/H.. cell_66082
cell_30702 5 E8.5 Erythroid3 cell_138114
cell_30703 5 E8.0 Doublet cell_92644
doub.density sizeFactor
<numeric> <numeric>
cell_9769 0.02985045 1.41243
cell_9770 0.00172753 1.22757
cell_9771 0.01338013 1.15439
cell_9772 0.00218402 1.28676
cell_9773 0.00211723 1.78719
... ... ...
cell_30699 0.00146287 0.389311
cell_30700 0.00374155 0.588784
cell_30701 0.05651258 0.624455
cell_30702 0.00108837 0.550807
cell_30703 0.82369305 1.184919For the sake of making these examples run faster, we drop some problematic types (stripped nuclei and doublets) and also randomly select 50% cells per sample.
R
drop <- sce$celltype.mapped %in% c("stripped", "Doublet")
sce <- sce[,!drop]
set.seed(29482)
idx <- unlist(tapply(colnames(sce), sce$sample, function(x) {
perc <- round(0.50 * length(x))
sample(x, perc)
}))
sce <- sce[,idx]
We now normalize the data, run some dimensionality reduction steps,
and visualize them in a tSNE plot. In this case we happen to have a ton
of cell types to visualize, so we define a custom palette with a lot of
visually distinct colors (adapted from the polychrome
palette in the pals
package).
R
sce <- logNormCounts(sce)
dec <- modelGeneVar(sce, block = sce$sample)
chosen.hvgs <- dec$bio > 0
sce <- runPCA(sce, subset_row = chosen.hvgs, ntop = 1000)
sce <- runTSNE(sce, dimred = "PCA")
sce$sample <- as.factor(sce$sample)
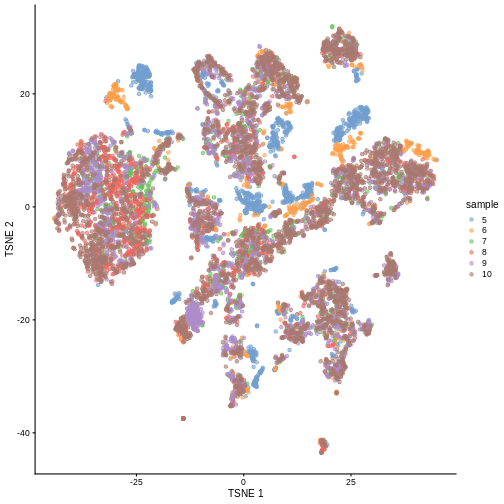
plotTSNE(sce, colour_by = "sample")
R
color_vec <- c("#5A5156", "#E4E1E3", "#F6222E", "#FE00FA", "#16FF32", "#3283FE",
"#FEAF16", "#B00068", "#1CFFCE", "#90AD1C", "#2ED9FF", "#DEA0FD",
"#AA0DFE", "#F8A19F", "#325A9B", "#C4451C", "#1C8356", "#85660D",
"#B10DA1", "#3B00FB", "#1CBE4F", "#FA0087", "#333333", "#F7E1A0",
"#C075A6", "#782AB6", "#AAF400", "#BDCDFF", "#822E1C", "#B5EFB5",
"#7ED7D1", "#1C7F93", "#D85FF7", "#683B79", "#66B0FF", "#FBE426")
plotTSNE(sce, colour_by = "celltype.mapped") +
scale_color_manual(values = color_vec) +
theme(legend.position = "bottom")
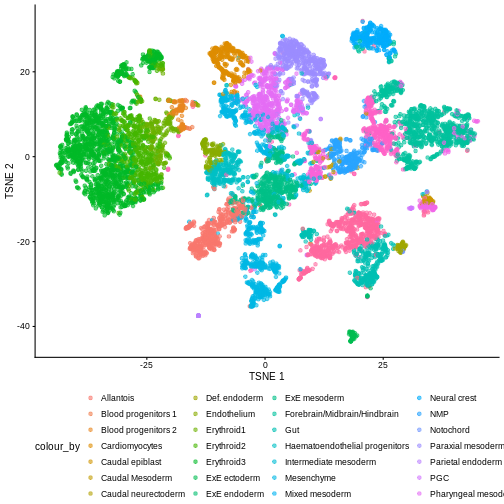
There are evident sample effects. Depending on the analysis that you want to perform you may want to remove or retain the sample effect. For instance, if the goal is to identify cell types with a clustering method, one may want to remove the sample effects with “batch effect” correction methods.
For now, let’s assume that we want to remove this effect.
Challenge
It seems like samples 5 and 6 are separated off from the others in gene expression space. Given the group of cells in each sample, why might this make sense versus some other pair of samples? What is the factor presumably leading to this difference?
Samples 5 and 6 were from the same “pool” of cells. Looking at the
documentation for the dataset under ?WTChimeraData we see
that the pool variable is defined as: “Integer, embryo pool from which
cell derived; samples with same value are matched.” So samples 5 and 6
have an experimental factor in common which causes a shared, systematic
difference in gene expression profiles compared to the other samples.
That’s why you can see many of isolated blue/orange clusters on the
first TSNE plot. If you were developing single-cell library preparation
protocols you might want to preserve this effect to understand how
variation in pools leads to variation in expression, but for now, given
that we’re investigating other effects, we’ll want to remove this as
undesired technical variation.
Correcting batch effects
We “correct” the effect of samples with the
correctExperiment function in the batchelor
package and using the sample column as batch.
R
set.seed(10102)
merged <- correctExperiments(
sce,
batch = sce$sample,
subset.row = chosen.hvgs,
PARAM = FastMnnParam(
merge.order = list(
list(1,3,5), # WT (3 replicates)
list(2,4,6) # td-Tomato (3 replicates)
)
)
)
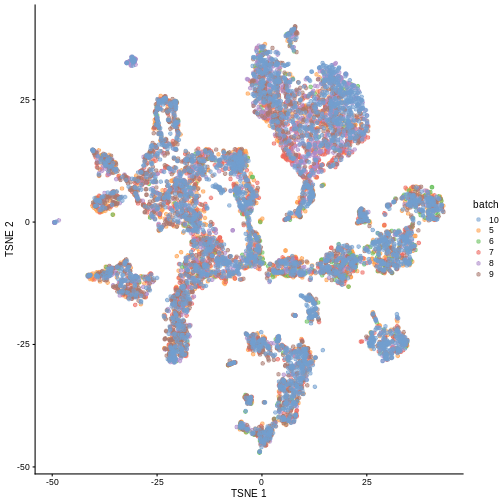
merged <- runTSNE(merged, dimred = "corrected")
plotTSNE(merged, colour_by = "batch")
We can also see that when coloring by cell type, the cell types are now nicely confined to their own clusters for the most part:
R
plotTSNE(merged, colour_by = "celltype.mapped") +
scale_color_manual(values = color_vec) +
theme(legend.position = "bottom")
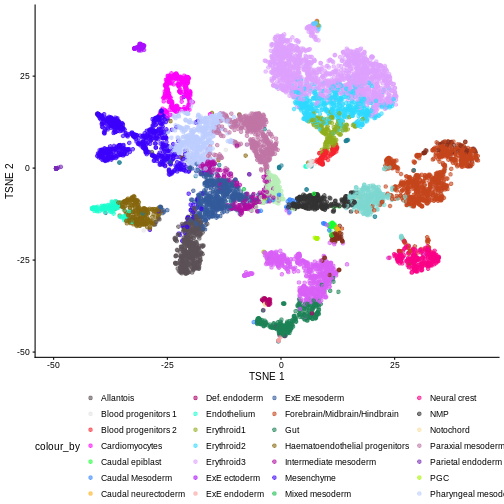
Once we removed the sample batch effect, we can proceed with the Differential Expression Analysis.
Challenge
True or False: after batch correction, no batch-level information is present in the corrected data.
False. Batch-level data can be retained through confounding with experimental factors or poor ability to distinguish experimental effects from batch effects. Remember, the changes needed to correct the data are empirically estimated, so they can carry along error.
While batch effect correction algorithms usually do a pretty good job, it’s smart to do a sanity check for batch effects at the end of your analysis. You always want to make sure that that effect you’re resting your paper submission on isn’t driven by batch effects.
Differential Expression
In order to perform a differential expression analysis, we need to identify groups of cells across samples/conditions (depending on the experimental design and the final aim of the experiment).
As previously seen, we have two ways of grouping cells, cell clustering and cell labeling. In our case we will focus on this second aspect to group cells according to the already annotated cell types to proceed with the computation of the pseudo-bulk samples.
Pseudo-bulk samples
To compute differences between groups of cells, a possible way is to compute pseudo-bulk samples, where we mediate the gene signal of all the cells for each specific cell type. In this manner, we are then able to detect differences between the same cell type across two different conditions.
To compute pseudo-bulk samples, we use the
aggregateAcrossCells function in the scuttle
package, which takes as input not only a SingleCellExperiment, but also
the id to use for the identification of the group of cells. In our case,
we use as id not just the cell type, but also the sample, because we
want be able to discern between replicates and conditions during further
steps.
R
# Using 'label' and 'sample' as our two factors; each column of the output
# corresponds to one unique combination of these two factors.
summed <- aggregateAcrossCells(
merged,
id = colData(merged)[,c("celltype.mapped", "sample")]
)
summed
OUTPUT
class: SingleCellExperiment
dim: 13641 179
metadata(2): merge.info pca.info
assays(1): counts
rownames(13641): ENSMUSG00000051951 ENSMUSG00000025900 ...
ENSMUSG00000096730 ENSMUSG00000095742
rowData names(3): rotation ENSEMBL SYMBOL
colnames: NULL
colData names(15): batch cell ... sample ncells
reducedDimNames(5): corrected pca.corrected.E7.5 pca.corrected.E8.5 PCA
TSNE
mainExpName: NULL
altExpNames(0):Differential Expression Analysis
The main advantage of using pseudo-bulk samples is the possibility to
use well-tested methods for differential analysis like
edgeR and DESeq2, we will focus on the former
for this analysis. edgeR and DESeq2 both use
negative binomial models under the hood, but differ in their
normalization strategies and other implementation details.
First, let’s start with a specific cell type, for instance the
“Mesenchymal stem cells”, and look into differences between this cell
type across conditions. We put the counts table into a
DGEList container called y, along with the
corresponding metadata.
R
current <- summed[, summed$celltype.mapped == "Mesenchyme"]
y <- DGEList(counts(current), samples = colData(current))
y
OUTPUT
An object of class "DGEList"
$counts
Sample1 Sample2 Sample3 Sample4 Sample5 Sample6
ENSMUSG00000051951 2 0 0 0 1 0
ENSMUSG00000025900 0 0 0 0 0 0
ENSMUSG00000025902 4 0 2 0 3 6
ENSMUSG00000033845 765 130 508 213 781 305
ENSMUSG00000002459 2 0 1 0 0 0
13636 more rows ...
$samples
group lib.size norm.factors batch cell barcode sample stage tomato pool
Sample1 1 2478901 1 5 <NA> <NA> 5 E8.5 TRUE 3
Sample2 1 548407 1 6 <NA> <NA> 6 E8.5 FALSE 3
Sample3 1 1260187 1 7 <NA> <NA> 7 E8.5 TRUE 4
Sample4 1 578699 1 8 <NA> <NA> 8 E8.5 FALSE 4
Sample5 1 2092329 1 9 <NA> <NA> 9 E8.5 TRUE 5
Sample6 1 904929 1 10 <NA> <NA> 10 E8.5 FALSE 5
stage.mapped celltype.mapped closest.cell doub.density sizeFactor
Sample1 <NA> Mesenchyme <NA> NA NA
Sample2 <NA> Mesenchyme <NA> NA NA
Sample3 <NA> Mesenchyme <NA> NA NA
Sample4 <NA> Mesenchyme <NA> NA NA
Sample5 <NA> Mesenchyme <NA> NA NA
Sample6 <NA> Mesenchyme <NA> NA NA
celltype.mapped.1 sample.1 ncells
Sample1 Mesenchyme 5 151
Sample2 Mesenchyme 6 28
Sample3 Mesenchyme 7 127
Sample4 Mesenchyme 8 75
Sample5 Mesenchyme 9 239
Sample6 Mesenchyme 10 146A typical step is to discard low quality samples due to low sequenced library size. We discard these samples because they can affect further steps like normalization and/or DEGs analysis.
We can see that in our case we don’t have low quality samples and we don’t need to filter out any of them.
R
discarded <- current$ncells < 10
y <- y[,!discarded]
summary(discarded)
OUTPUT
Mode FALSE
logical 6 The same idea is typically applied to the genes, indeed we need to discard low expressed genes to improve accuracy for the DEGs modeling.
R
keep <- filterByExpr(y, group = current$tomato)
y <- y[keep,]
summary(keep)
OUTPUT
Mode FALSE TRUE
logical 9121 4520 We can now proceed to normalize the data. There are several
approaches for normalizing bulk, and hence pseudo-bulk data. Here, we
use the Trimmed Mean of M-values method, implemented in the
edgeR package within the calcNormFactors
function. Keep in mind that because we are going to normalize the
pseudo-bulk counts, we don’t need to normalize the data in “single cell
form”.
R
y <- calcNormFactors(y)
y$samples
OUTPUT
group lib.size norm.factors batch cell barcode sample stage tomato pool
Sample1 1 2478901 1.0506857 5 <NA> <NA> 5 E8.5 TRUE 3
Sample2 1 548407 1.0399112 6 <NA> <NA> 6 E8.5 FALSE 3
Sample3 1 1260187 0.9700083 7 <NA> <NA> 7 E8.5 TRUE 4
Sample4 1 578699 0.9871129 8 <NA> <NA> 8 E8.5 FALSE 4
Sample5 1 2092329 0.9695559 9 <NA> <NA> 9 E8.5 TRUE 5
Sample6 1 904929 0.9858611 10 <NA> <NA> 10 E8.5 FALSE 5
stage.mapped celltype.mapped closest.cell doub.density sizeFactor
Sample1 <NA> Mesenchyme <NA> NA NA
Sample2 <NA> Mesenchyme <NA> NA NA
Sample3 <NA> Mesenchyme <NA> NA NA
Sample4 <NA> Mesenchyme <NA> NA NA
Sample5 <NA> Mesenchyme <NA> NA NA
Sample6 <NA> Mesenchyme <NA> NA NA
celltype.mapped.1 sample.1 ncells
Sample1 Mesenchyme 5 151
Sample2 Mesenchyme 6 28
Sample3 Mesenchyme 7 127
Sample4 Mesenchyme 8 75
Sample5 Mesenchyme 9 239
Sample6 Mesenchyme 10 146To investigate the effect of our normalization, we use a Mean-Difference (MD) plot for each sample in order to detect possible normalization problems due to insufficient cells/reads/UMIs composing a particular pseudo-bulk profile.
In our case, we verify that all these plots are centered in 0 (on y-axis) and present a trumpet shape, as expected.
R
par(mfrow = c(2,3))
for (i in seq_len(ncol(y))) {
plotMD(y, column = i)
}
R
par(mfrow = c(1,1))
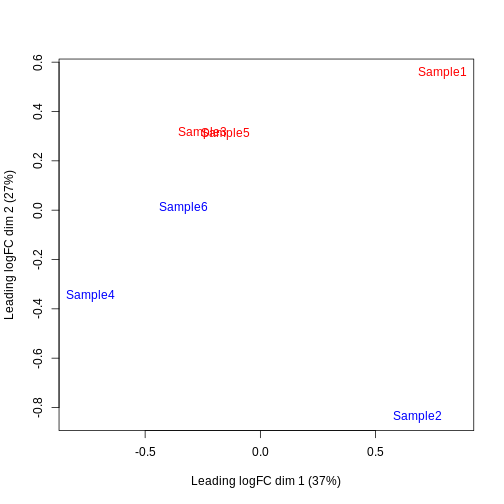
Furthermore, we want to check if the samples cluster together based on their known factors (like the tomato injection in this case).
In this case, we’ll use the multidimensional scaling (MDS) plot. Multidimensional scaling (which also goes by principal coordinate analysis (PCoA)) is a dimensionality reduction technique that’s conceptually similar to principal component analysis (PCA).
R
limma::plotMDS(cpm(y, log = TRUE),
col = ifelse(y$samples$tomato, "red", "blue"))
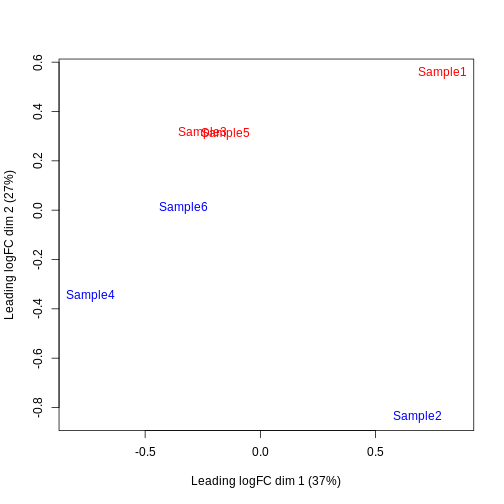
We then construct a design matrix by including both the pool and the tomato as factors. This design indicates which samples belong to which pool and condition, so we can use it in the next step of the analysis.
R
design <- model.matrix(~factor(pool) + factor(tomato),
data = y$samples)
design
OUTPUT
(Intercept) factor(pool)4 factor(pool)5 factor(tomato)TRUE
Sample1 1 0 0 1
Sample2 1 0 0 0
Sample3 1 1 0 1
Sample4 1 1 0 0
Sample5 1 0 1 1
Sample6 1 0 1 0
attr(,"assign")
[1] 0 1 1 2
attr(,"contrasts")
attr(,"contrasts")$`factor(pool)`
[1] "contr.treatment"
attr(,"contrasts")$`factor(tomato)`
[1] "contr.treatment"Now we can estimate the Negative Binomial (NB) overdispersion parameter, to model the mean-variance trend.
R
y <- estimateDisp(y, design)
summary(y$trended.dispersion)
OUTPUT
Min. 1st Qu. Median Mean 3rd Qu. Max.
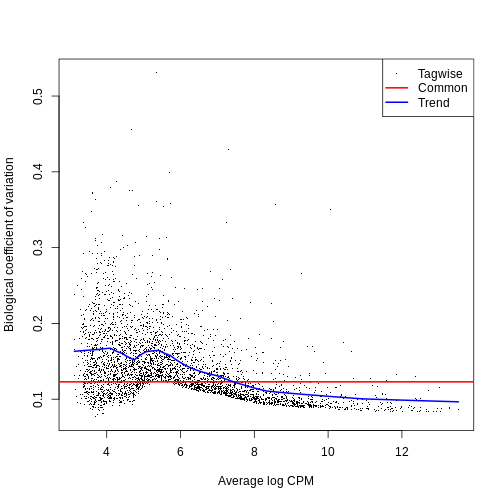
0.009325 0.016271 0.024233 0.021603 0.026868 0.027993 The BCV plot allows us to investigate the relation between the
Biological Coefficient of Variation and the Average log CPM for each
gene. Additionally, the Common and Trend BCV are shown in
red and blue.
R
plotBCV(y)
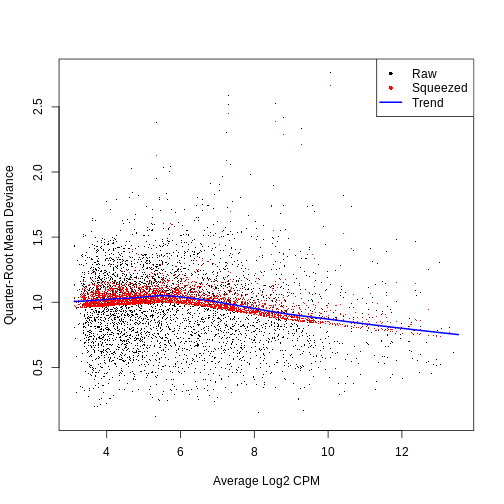
We then fit a Quasi-Likelihood (QL) negative binomial generalized
linear model for each gene. The robust = TRUE parameter
avoids distortions from highly variable clusters. The QL method includes
an additional dispersion parameter, useful to handle the uncertainty and
variability of the per-gene variance, which is not well estimated by the
NB dispersions, so the two dispersion types complement each other in the
final analysis.
R
fit <- glmQLFit(y, design, robust = TRUE)
summary(fit$var.prior)
OUTPUT
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.3189 0.9705 1.0901 1.0251 1.1486 1.2151 R
summary(fit$df.prior)
OUTPUT
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.3046 8.7242 8.7242 8.6466 8.7242 8.7242 QL dispersion estimates for each gene as a function of abundance. Raw estimates (black) are shrunk towards the trend (blue) to yield squeezed estimates (red).
R
plotQLDisp(fit)
We then use an empirical Bayes quasi-likelihood F-test to test for differential expression (due to tomato injection) per each gene at a False Discovery Rate (FDR) of 5%. The low amount of DGEs highlights that the tomato injection effect has a low influence on the mesenchyme cells.
R
res <- glmQLFTest(fit, coef = ncol(design))
summary(decideTests(res))
OUTPUT
factor(tomato)TRUE
Down 5
NotSig 4510
Up 5R
topTags(res)
OUTPUT
Coefficient: factor(tomato)TRUE
logFC logCPM F PValue FDR
ENSMUSG00000010760 -4.1515323 9.973704 1118.17411 3.424939e-12 1.548073e-08
ENSMUSG00000096768 1.9987246 8.844258 375.41194 1.087431e-09 2.457594e-06
ENSMUSG00000035299 1.7963926 6.904163 119.08173 3.853318e-07 5.805666e-04
ENSMUSG00000086503 -6.4701526 7.411257 238.72531 1.114877e-06 1.259812e-03
ENSMUSG00000101609 1.3784805 7.310009 79.94279 2.682051e-06 2.424574e-03
ENSMUSG00000019188 -1.0191494 7.545530 62.01494 8.860823e-06 6.675153e-03
ENSMUSG00000024423 0.9940616 7.391075 56.84876 1.322645e-05 8.540506e-03
ENSMUSG00000042607 -0.9508732 7.468203 45.43086 3.625976e-05 2.048676e-02
ENSMUSG00000036446 -0.8280894 9.401028 43.03008 4.822988e-05 2.293136e-02
ENSMUSG00000027520 1.5929714 6.952923 42.86686 5.073310e-05 2.293136e-02All the previous steps can be easily performed with the following
function for each cell type, thanks to the pseudoBulkDGE
function in the scran package.
R
summed.filt <- summed[,summed$ncells >= 10]
de.results <- pseudoBulkDGE(
summed.filt,
label = summed.filt$celltype.mapped,
design = ~factor(pool) + tomato,
coef = "tomatoTRUE",
condition = summed.filt$tomato
)
The returned object is a list of DataFrames each with
the results for a cell type. Each of these contains also the
intermediate results in edgeR format to perform any
intermediate plot or diagnostic.
R
cur.results <- de.results[["Allantois"]]
cur.results[order(cur.results$PValue),]
OUTPUT
DataFrame with 13641 rows and 5 columns
logFC logCPM F PValue FDR
<numeric> <numeric> <numeric> <numeric> <numeric>
ENSMUSG00000037664 -7.993129 11.55290 2730.230 1.05747e-13 4.44242e-10
ENSMUSG00000010760 -2.575007 12.40592 1049.284 1.33098e-11 2.79572e-08
ENSMUSG00000086503 -7.015618 7.49749 788.150 5.88102e-11 8.23539e-08
ENSMUSG00000096768 1.828366 9.33239 343.044 3.58836e-09 3.76868e-06
ENSMUSG00000022464 0.970431 10.28302 126.467 4.59369e-07 3.85961e-04
... ... ... ... ... ...
ENSMUSG00000095247 NA NA NA NA NA
ENSMUSG00000096808 NA NA NA NA NA
ENSMUSG00000079808 NA NA NA NA NA
ENSMUSG00000096730 NA NA NA NA NA
ENSMUSG00000095742 NA NA NA NA NAChallenge
Clearly some of the results have low p-values. What about the effect
sizes? What does logFC stand for?
“logFC” stands for log fold-change. edgeR uses a log2
convention. Rather than reporting e.g. a 5-fold increase, it’s better to
report a logFC of log2(5) = 2.32. Additive log scales are easier to work
with than multiplicative identity scales, once you get used to it.
ENSMUSG00000037664 seems to have an estimated logFC of
about -8. That’s a big difference if it’s real.
Differential Abundance
With DA we look for differences in cluster abundance across conditions (the tomato injection in our case), rather than differences in gene expression.
Our first steps are quantifying the number of cells per each cell type and fitting a model to catch differences between the injected cells and the background.
The process is very similar differential expression modeling, but this time we start our analysis on the computed abundances and without normalizing the data with TMM.
R
abundances <- table(merged$celltype.mapped, merged$sample)
abundances <- unclass(abundances)
extra.info <- colData(merged)[match(colnames(abundances), merged$sample),]
y.ab <- DGEList(abundances, samples = extra.info)
design <- model.matrix(~factor(pool) + factor(tomato), y.ab$samples)
y.ab <- estimateDisp(y.ab, design, trend = "none")
fit.ab <- glmQLFit(y.ab, design, robust = TRUE, abundance.trend = FALSE)
Background on compositional effect
As mentioned before, in DA we don’t normalize our data with
calcNormFactors function, because this approach considers
that most of the input features do not vary between conditions. This
cannot be applied to DA analysis because we have a small number of cell
populations that all can change due to the treatment. This means that
here we will normalize only for library depth, which in pseudo-bulk data
means by the total number of cells in each sample (cell type).
On the other hand, this can lead our data to be susceptible to compositional effect. “Compositional” refers to the fact that the cluster abundances in a sample are not independent of one another because each cell type is effectively competing for space in the sample. They behave like proportions in that they must sum to 1. If cell type A abundance increases in a new condition, that means we’ll observe less of everything else, even if everything else is unaffected by the new condition.
Compositionality means that our conclusions can be biased by the amount of cells present in each cell type. And this amount of cells can be totally unbalanced between cell types. This is particularly problematic for cell types that start at or end up near 0 or 100 percent.
For example, a specific cell type can be 40% of the total amount of cells present in the experiment, while another just the 3%. The differences in terms of abundance of these cell types are detected between the different conditions, but our final interpretation could be biased if we don’t consider this aspect.
We now look at different approaches for handling the compositional effect.
Assuming most labels do not change
We can use a similar approach used during the DEGs analysis, assuming that most labels are not changing, in particular if we think about the low number of DEGs resulted from the previous analysis.
To do so, we first normalize the data with
calcNormFactors and then we fit and estimate a QL-model for
our abundance data.
R
y.ab2 <- calcNormFactors(y.ab)
y.ab2$samples$norm.factors
OUTPUT
[1] 1.1029040 1.0228173 1.0695358 0.7686501 1.0402941 1.0365354We then use edgeR in a manner similar to what we ran before:
R
y.ab2 <- estimateDisp(y.ab2, design, trend = "none")
fit.ab2 <- glmQLFit(y.ab2, design, robust = TRUE, abundance.trend = FALSE)
res2 <- glmQLFTest(fit.ab2, coef = ncol(design))
summary(decideTests(res2))
OUTPUT
factor(tomato)TRUE
Down 4
NotSig 29
Up 1R
topTags(res2, n = 10)
OUTPUT
Coefficient: factor(tomato)TRUE
logFC logCPM F PValue FDR
ExE ectoderm -5.7983253 13.13490 34.326044 1.497957e-07 5.093053e-06
Parietal endoderm -6.9219242 12.36649 21.805721 1.468320e-05 2.496144e-04
Erythroid3 -0.9115099 17.34677 12.478845 7.446554e-04 8.439428e-03
Mesenchyme 0.9796446 16.32654 11.692412 1.064808e-03 9.050865e-03
Neural crest -1.0469872 14.83912 7.956363 6.274678e-03 4.266781e-02
Endothelium 0.9241543 14.12195 4.437179 3.885736e-02 2.201917e-01
Erythroid2 -0.6029365 15.97357 3.737927 5.735479e-02 2.682206e-01
Cardiomyocytes 0.6789803 14.93321 3.569604 6.311073e-02 2.682206e-01
ExE endoderm -3.9996258 10.75172 3.086597 8.344133e-02 3.125815e-01
Allantois 0.5462287 15.54924 2.922074 9.193574e-02 3.125815e-01Testing against a log-fold change threshold
A second approach assumes that the composition bias introduces a spurious log2-fold change of no more than a quantity for a non-DA label.
In other words, we interpret this as the maximum log-fold change in the total number of cells given by DA in other labels. On the other hand, when choosing , we should not consider fold-differences in the totals due to differences in capture efficiency or the size of the original cell population are not attributable to composition bias. We then mitigate the effect of composition biases by testing each label for changes in abundance beyond .
R
res.lfc <- glmTreat(fit.ab, coef = ncol(design), lfc = 1)
summary(decideTests(res.lfc))
OUTPUT
factor(tomato)TRUE
Down 2
NotSig 32
Up 0R
topTags(res.lfc)
OUTPUT
Coefficient: factor(tomato)TRUE
logFC unshrunk.logFC logCPM PValue
ExE ectoderm -5.5156915 -5.9427658 13.06465 5.730409e-06
Parietal endoderm -6.5897795 -27.4235942 12.30091 1.215896e-04
ExE endoderm -3.9307381 -23.9369433 10.76159 7.352966e-02
Mesenchyme 1.1615857 1.1628182 16.35239 1.335104e-01
Endothelium 1.0564619 1.0620564 14.14422 2.136590e-01
Caudal neurectoderm -1.4588627 -1.6095620 11.09613 3.257325e-01
Cardiomyocytes 0.8521199 0.8545967 14.96579 3.649535e-01
Neural crest -0.8366836 -0.8392250 14.83184 3.750471e-01
Def. endoderm 0.7335519 0.7467590 12.50001 4.219471e-01
Allantois 0.7637525 0.7650565 15.54528 4.594987e-01
FDR
ExE ectoderm 0.0001948339
Parietal endoderm 0.0020670230
ExE endoderm 0.8333361231
Mesenchyme 0.9866105512
Endothelium 0.9866105512
Caudal neurectoderm 0.9866105512
Cardiomyocytes 0.9866105512
Neural crest 0.9866105512
Def. endoderm 0.9866105512
Allantois 0.9866105512Addionally, the choice of can be guided by other external experimental data, like a previous or a pilot experiment.
Exercises
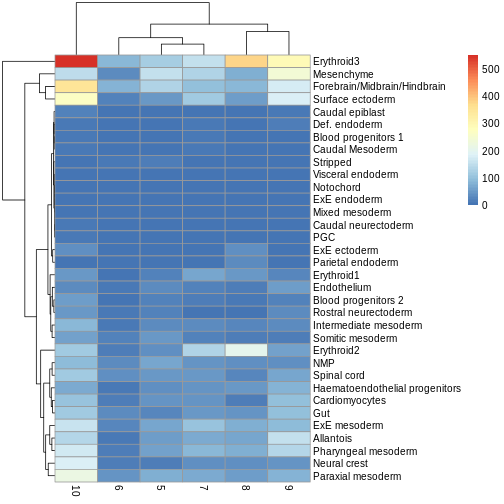
Exercise 1: Heatmaps
Use the pheatmap package to create a heatmap of the
abundances table. Does it comport with the model results?
You can simply hand pheatmap() a matrix as its only
argument. pheatmap() has a million options you can adjust,
but the defaults are usually pretty good. Try to overlay sample-level
information with the annotation_col argument for an extra
challenge.
R
pheatmap(y.ab$counts)
R
anno_df <- y.ab$samples[,c("tomato", "pool")]
anno_df$pool = as.character(anno_df$pool)
anno_df$tomato <- ifelse(anno_df$tomato,
"tomato+",
"tomato-")
pheatmap(y.ab$counts,
annotation_col = anno_df)
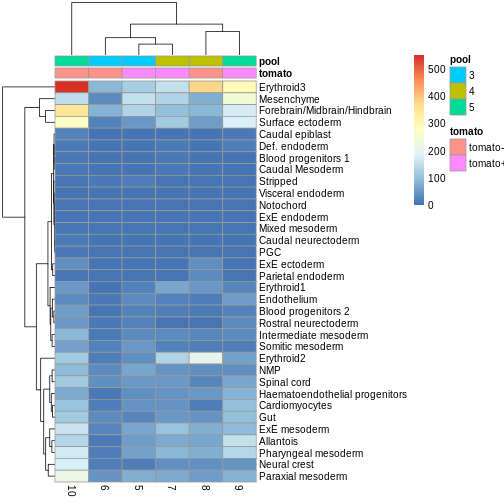
The top DA result was a decrease in ExE ectoderm in the tomato
condition, which you can sort of see, especially if you
log1p() the counts or discard rows that show much higher
values. ExE ectoderm counts were much higher in samples 8 and 10
compared to 5, 7, and 9.
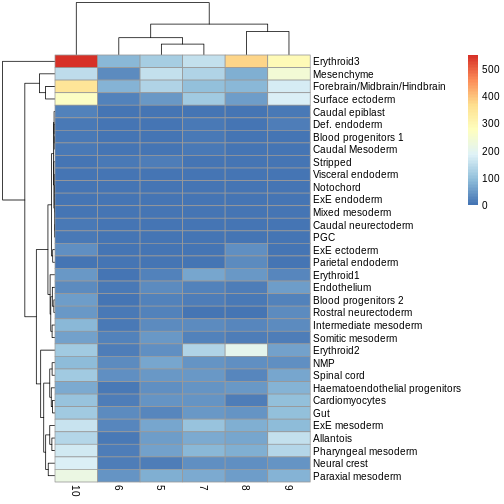
Exercise 2: Model specification and comparison
Try re-running the pseudobulk DGE without the pool
factor in the design specification. Compare the logFC estimates and the
distribution of p-values for the Erythroid3 cell type.
After running the second pseudobulk DGE, you can join the two
DataFrames of Erythroid3 statistics using the
merge() function. You will need to create a common key
column from the gene IDs.
R
de.results2 <- pseudoBulkDGE(
summed.filt,
label = summed.filt$celltype.mapped,
design = ~tomato,
coef = "tomatoTRUE",
condition = summed.filt$tomato
)
eryth1 <- de.results$Erythroid3
eryth2 <- de.results2$Erythroid3
eryth1$gene <- rownames(eryth1)
eryth2$gene <- rownames(eryth2)
comp_df <- merge(eryth1, eryth2, by = 'gene')
comp_df <- comp_df[!is.na(comp_df$logFC.x),]
ggplot(comp_df, aes(logFC.x, logFC.y)) +
geom_abline(lty = 2, color = "grey") +
geom_point()
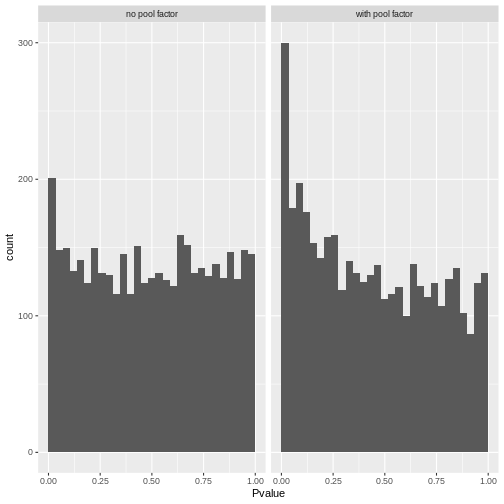
R
# Reshape to long format for ggplot facets. This is 1000x times easier to do
# with tidyverse packages:
pval_df <- reshape(comp_df[,c("gene", "PValue.x", "PValue.y")],
direction = "long",
v.names = "Pvalue",
timevar = "pool_factor",
times = c("with pool factor", "no pool factor"),
varying = c("PValue.x", "PValue.y"))
ggplot(pval_df, aes(Pvalue)) +
geom_histogram(boundary = 0,
bins = 30) +
facet_wrap("pool_factor")
We can see that in this case, the logFC estimates are strongly
consistent between the two models, which tells us that the inclusion of
the pool factor in the model doesn’t strongly influence the
estimate of the tomato coefficients in this case.
The p-value histograms both look alright here, with a largely flat
plateau over most of the 0 - 1 range and a spike near 0. This is
consistent with the hypothesis that most genes are unaffected by
tomato but there are a small handful that clearly are.
If there were large shifts in the logFC estimates or p-value distributions, that’s a sign that the design specification change has a large impact on how the model sees the data. If that happens, you’ll need to think carefully and critically about what variables should and should not be included in the model formula.
Extension challenge 1: Group effects
Having multiple independent samples in each experimental group is always helpful, but it’s particularly important when it comes to batch effect correction. Why?
It’s important to have multiple samples within each experimental group because it helps the batch effect correction algorithm distinguish differences due to batch effects (uninteresting) from differences due to group/treatment/biology (interesting).
Imagine you had one sample that received a drug treatment and one that did not, each with 10,000 cells. They differ substantially in expression of gene X. Is that an important scientific finding? You can’t tell for sure, because the effect of drug is indistinguishable from a sample-wise batch effect. But if the difference in gene X holds up when you have five treated samples and five untreated samples, now you can be a bit more confident. Many batch effect correction methods will take information on experimental factors as additional arguments, which they can use to help remove batch effects while retaining experimental differences.
Further Reading
- OSCA book, Multi-sample analysis, Chapters 1, 4, and 6
Key Points
- Batch effects are systematic technical differences in the observed expression in cells measured in different experimental batches.
- Computational removal of batch-to-batch variation with the
correctExperimentfunction from the batchelor package allows us to combine data across multiple batches for a consolidated downstream analysis. - Differential expression (DE) analysis of replicated multi-condition scRNA-seq experiments is typically based on pseudo-bulk expression profiles, generated by summing counts for all cells with the same combination of label and sample.
- The
aggregateAcrossCellsfunction from the scater package facilitates the creation of pseudo-bulk samples. - The
pseudoBulkDGEfunction from the scran package can be used to detect significant changes in expression between conditions for pseudo-bulk samples consisting of cells of the same type. - Differential abundance (DA) analysis aims at identifying significant changes in cell type abundance across conditions.
- DA analysis uses bulk DE methods such as edgeR and DESeq2, which provide suitable statistical models for count data in the presence of limited replication - except that the counts are not of reads per gene, but of cells per label.
Session Info
R
sessionInfo()
OUTPUT
R version 4.4.1 (2024-06-14)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 22.04.5 LTS
Matrix products: default
BLAS: /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.10.0
LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.10.0
locale:
[1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8
[4] LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8
[7] LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C
[10] LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C
time zone: UTC
tzcode source: system (glibc)
attached base packages:
[1] stats4 stats graphics grDevices utils datasets methods
[8] base
other attached packages:
[1] pheatmap_1.0.12 scran_1.32.0
[3] scater_1.32.0 ggplot2_3.5.1
[5] scuttle_1.14.0 edgeR_4.2.0
[7] limma_3.60.2 batchelor_1.20.0
[9] MouseGastrulationData_1.18.0 SpatialExperiment_1.14.0
[11] SingleCellExperiment_1.26.0 SummarizedExperiment_1.34.0
[13] Biobase_2.64.0 GenomicRanges_1.56.0
[15] GenomeInfoDb_1.40.1 IRanges_2.38.0
[17] S4Vectors_0.42.0 BiocGenerics_0.50.0
[19] MatrixGenerics_1.16.0 matrixStats_1.3.0
[21] BiocStyle_2.32.0
loaded via a namespace (and not attached):
[1] RColorBrewer_1.1-3 jsonlite_1.8.8
[3] magrittr_2.0.3 ggbeeswarm_0.7.2
[5] magick_2.8.3 farver_2.1.2
[7] rmarkdown_2.27 zlibbioc_1.50.0
[9] vctrs_0.6.5 memoise_2.0.1
[11] DelayedMatrixStats_1.26.0 htmltools_0.5.8.1
[13] S4Arrays_1.4.1 AnnotationHub_3.12.0
[15] curl_5.2.1 BiocNeighbors_1.22.0
[17] SparseArray_1.4.8 cachem_1.1.0
[19] ResidualMatrix_1.14.0 igraph_2.0.3
[21] mime_0.12 lifecycle_1.0.4
[23] pkgconfig_2.0.3 rsvd_1.0.5
[25] Matrix_1.7-0 R6_2.5.1
[27] fastmap_1.2.0 GenomeInfoDbData_1.2.12
[29] digest_0.6.35 colorspace_2.1-0
[31] AnnotationDbi_1.66.0 dqrng_0.4.1
[33] irlba_2.3.5.1 ExperimentHub_2.12.0
[35] RSQLite_2.3.7 beachmat_2.20.0
[37] filelock_1.0.3 labeling_0.4.3
[39] fansi_1.0.6 httr_1.4.7
[41] abind_1.4-5 compiler_4.4.1
[43] bit64_4.0.5 withr_3.0.0
[45] BiocParallel_1.38.0 viridis_0.6.5
[47] DBI_1.2.3 highr_0.11
[49] rappdirs_0.3.3 DelayedArray_0.30.1
[51] rjson_0.2.21 bluster_1.14.0
[53] tools_4.4.1 vipor_0.4.7
[55] beeswarm_0.4.0 glue_1.7.0
[57] grid_4.4.1 Rtsne_0.17
[59] cluster_2.1.6 generics_0.1.3
[61] gtable_0.3.5 BiocSingular_1.20.0
[63] ScaledMatrix_1.12.0 metapod_1.12.0
[65] utf8_1.2.4 XVector_0.44.0
[67] ggrepel_0.9.5 BiocVersion_3.19.1
[69] pillar_1.9.0 BumpyMatrix_1.12.0
[71] splines_4.4.1 dplyr_1.1.4
[73] BiocFileCache_2.12.0 lattice_0.22-6
[75] renv_1.0.11 bit_4.0.5
[77] tidyselect_1.2.1 locfit_1.5-9.9
[79] Biostrings_2.72.1 knitr_1.47
[81] gridExtra_2.3 xfun_0.44
[83] statmod_1.5.0 UCSC.utils_1.0.0
[85] yaml_2.3.8 evaluate_0.23
[87] codetools_0.2-20 tibble_3.2.1
[89] BiocManager_1.30.23 cli_3.6.2
[91] munsell_0.5.1 Rcpp_1.0.12
[93] dbplyr_2.5.0 png_0.1-8
[95] parallel_4.4.1 blob_1.2.4
[97] sparseMatrixStats_1.16.0 viridisLite_0.4.2
[99] scales_1.3.0 purrr_1.0.2
[101] crayon_1.5.2 rlang_1.1.3
[103] cowplot_1.1.3 KEGGREST_1.44.0
[105] formatR_1.14 